Diffusion Limited Aggregation

Figure 1.Diffusion Limited Aggregation Graphic

Over the weekend I spent some time experimenting with Diffusion Limited Aggregation. In computer graphics Diffusion Limited Aggregation is a method for growing or creating shapes that have a nature-made quality and which have a fractal dimension. In nature, this type of growth is seen in coral reefs and crystals. Note the dendritic structure in the illustration above – which reminds me somewhat of ice crystals on a window pane. The concept's origin is with the paper Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon by T. A. Witten and L. M. Sander that appeared in an 1981 issue of Physical Review Letters.

The growth of structure seen when using the Diffusion Limited Aggregation method results from the random deposition of particles on a surface. The basic rule is that whenever a moving particle finds itself adjacent to a stationary particle, it too becomes stationary and a new moving particle is created to take its place. A typical growth simulation will start off with one or more seed particles – particles which are already stationary. A number of moving particles are then added to the system. The movement of the individual particles is random.

The random motion that the particles undergo is described as a random walk. The path that an individual particle takes is determined by a random process with the two components being direction and distance (think vector). In my implementation of random motion, collisions between moving particles was ignored. The nature of the random walk is related to Brownian motion. Brownian motion is the type of movement exhibited by particles suspended in a liquid medium. Figure 2 below shows the random motion of three particles using the same algorithm as used in the Diffusion Limited Aggregation process that created the growth in the Figure 1.

Brownian Motion example
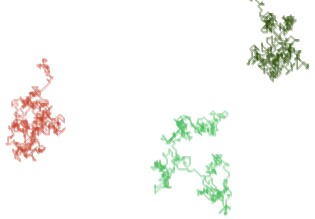
Figure 2.An example of Brownian Motion

As you can see in Figure 1, the Diffusion Limited Aggregation growth is rather symmetrical. This particular growth would have been more symmetrical except that there were additional growths, cropped out of the image shown, that captured particles that would have otherwise been deposited on the growths shown. There are several other ways to obtain non-symmetrical growths. One method for achieving directional growth is by omitting one or more of the eight moveable directions on the rectangular grid. Another method would be a preferential bias in the detection of adjacent stationary particles.

Diffusion Limited Aggregation can be a very inefficient way, in terms of CPU cycles, to generate growths. Depending on the size of the playing field, the number of seeded stationary particles, and the number and nature of the living particles, a Diffusion Limited Aggregation algorithm can take quite a long time to create a growth of any meaningful size.

Writing a program to create imagery using Diffusion Limited Aggregation was instructive but I do not know whether or not I will ever make artistic use of this technique. However, I have yet to attempt a 3D version which should offer greater artistic possibilities.

For further information see:

| Return to the Blog Index | This entry was posted on Thursday, August 27th, 2009 at 9:18 pm and is filed under Algorithmic Art, Digital Art.